数学常识:那些毕业后也不应该忘记的数学
约 899 字大约 3 分钟
2026-01-28
说来惭愧,毕业多年,在看一个讲统计思维的视频时,其中提到了“方差”,愣是好久没想起来我们小学二年级就学过的“方差”是什么,它解决什么问题。所以有了这一篇。
平均数、中位数、众数
平均数(Mean)是一组数字的总和除以数量,它是总量的平均分配,也就是说,如果大家平分,每个人可以有多少。平均数有一个致命的缺陷是容易被极端数据带偏,例如“我和马云平均每人有上亿资产”。
中位数(Median)是在一组数字中,位于最中间的那个数,它告诉我们处于中间水平的人是什么样的。因为它正好在中间,所以不太会被极端数据扭曲。
众数(Mode)是一组数字中,出现次数最多的那个数字,它告诉我们哪种情况最常见,例如平均鞋码没有意义,而最多人穿的鞋码才是我们要关注的。
方差、标准差
平均值具有欺骗性,例如有以下两组数据,这两组数据的平均值都是50,但显然 A 组非常稳定,而 B 组非常动荡。
A组:50, 50, 50, 50, 50
B组:0, 20, 50, 80, 100方差和标准差的出现,就是为了量化这种“动荡”或“参差不齐”的程度。 如果一组数据的方差很大,那我们就说这组数据很不稳定。
方差的计算方法是:每个数据与平均值的差的平方和,再除以数据的个数。之所以要平方和,是为了消除正数和负数会相互抵消的问题。但是这样带来了单位的不一致,于是我们对方差开平方根,得到标准差。
总的来说,这两个差都是衡量数据的波动程度的,只不过方差在数学推导、统计建模中更方便,但在描述数据、做报告时标准差会更直观和易于理解。
正态分布
正态分布(Normal Distribution),也称为高斯分布(Gaussian Distribution)。它描述了一种“中间多、两头少”的数据分布形态。这种分布在自然界和人类社会中极为常见,从身高体重到考试成绩,许多数据都呈现这种分布规律。它说明了绝大多数数值都接近平均值,极端值(极大或极小)是非常罕见的。
中心极限定理(Central Limit Theorem):即使原始数据不服从正态分布,只要样本量足够大,样本均值的分布也会近似服从正态分布。
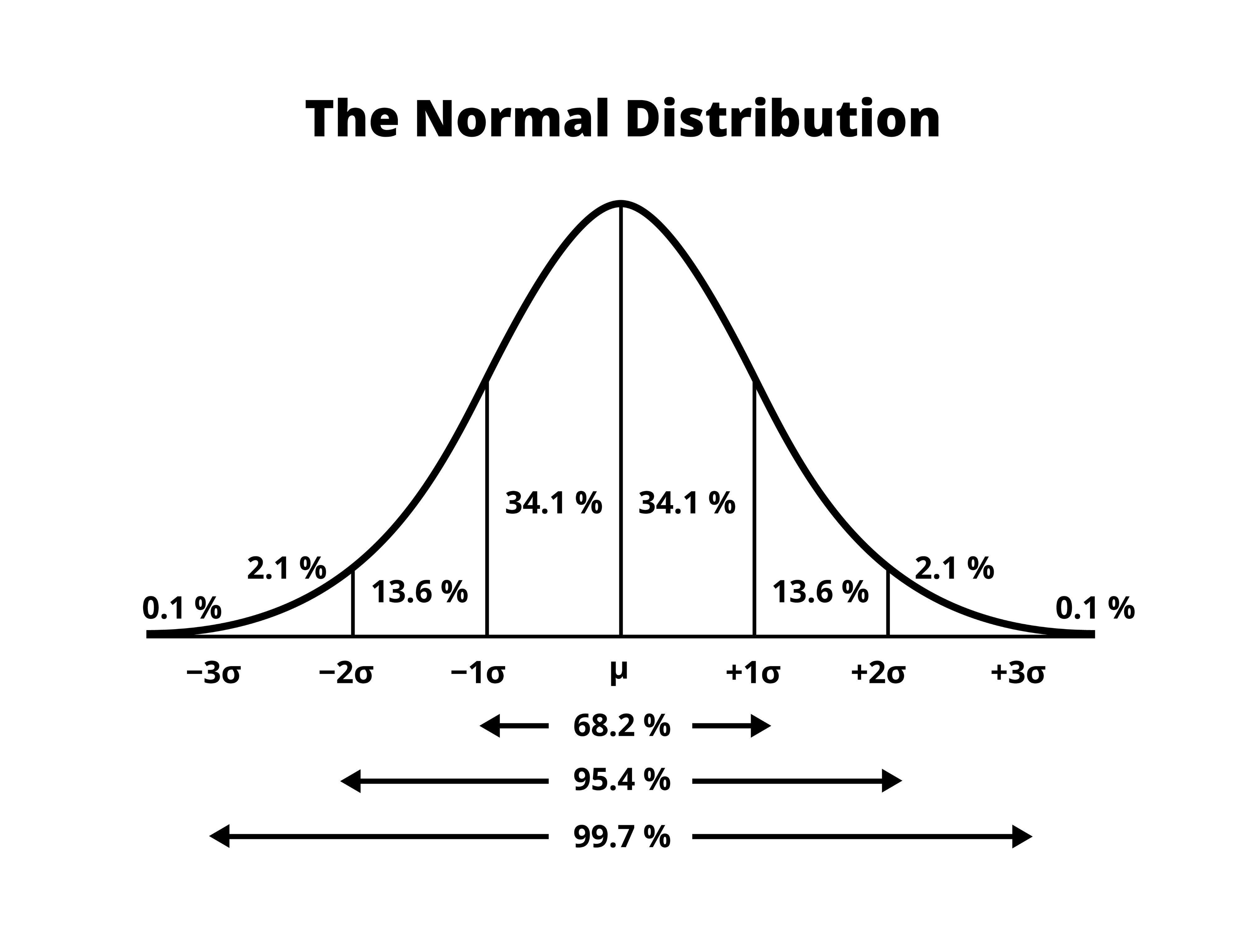
正态分布的应用:
- 异常检测:如果一个数值偏离平均值超过 3 个标准差(Sigma),它发生的概率极低(小于0.3%),通常被视为异常值或黑天鹅事件。
- 质量控制:如果生产线达到六西格玛(6 Sigma)标准,意味着次品率仅为百万分之 3.4;
- 科学研究:研究人员利用正态分布来判断实验结果是否具有统计学意义,而不是偶然发生的;
- 评分与标准化:智商(IQ)测试的设计就是为了让结果服从正态分布(均值 100,标准差 15)。这样我们就能知道 IQ 130 以上的人在人群中处于什么百分位(前2%)。
