优先队列和堆

约 1971 字大约 7 分钟

数据结构和算法

2018-04-12

优先队列

有时候我们会收集一些元素，然后处理最大的那个。然后再收集更多，再处理。例如，在手机来电、短信、游戏三个程序中，来电的优先级是最高的，我们总希望先处理来电请求。

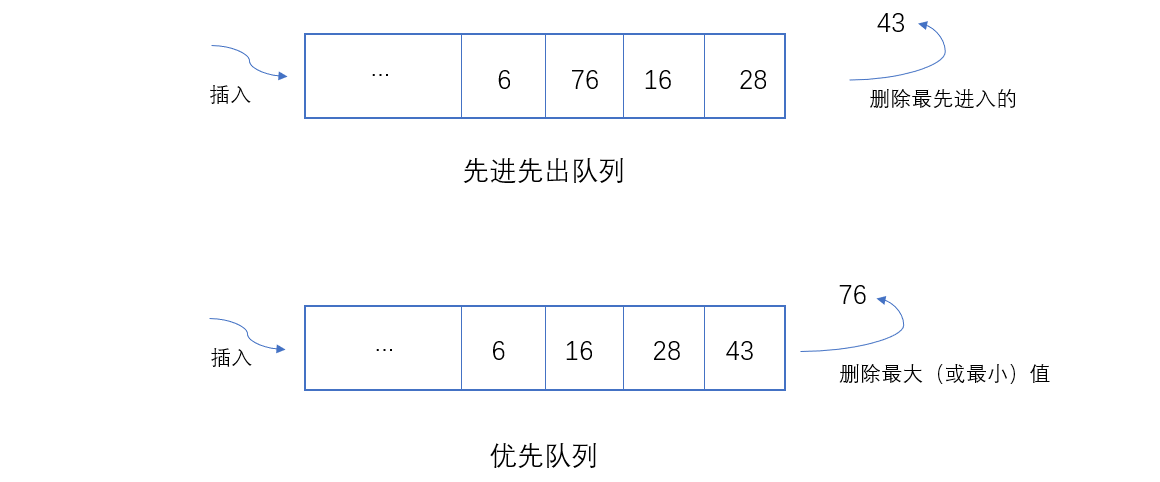
满足这种场景的数据结构，需要支持两种操作： 插入元素 和 删除最大（或最小）元素。这种数据类型，就叫优先队列。优先队列也是一种队列，但是跟前面提到的先进先出队列不同，优先队列的“出”，是根据优先级来的（最大或最小的先出）。

优先队列在很多地方有应用，例如：

数据压缩：哈夫曼编码算法
最短路径算法：Dijkstra算法
最小生成树算法：Prim算法
事件驱动仿真：顾客排队算法
选择问题：查找第k个（前k个）最小（最大）元素

优先队列的初级实现

使用无序数组实现

我们可以用栈来实现优先队列。只需要在其中加入一段内循环代码，将最大元素和栈顶元素交换，然后弹栈删除它。

使用有序数组实现

在插入操作中添加代码，将较大的元素往右边移动一格，以保证数组有序。这样，栈顶的元素永远是最大的，弹栈删除即可。

使用链表实现

可以用基于链表的下压栈。弹栈时，遍历链表找到并返回最大的元素，或者入栈时，先保证所有元素逆序，并用 pop() 删除并返回链表的首元素（最大元素）。

优先队列的堆实现

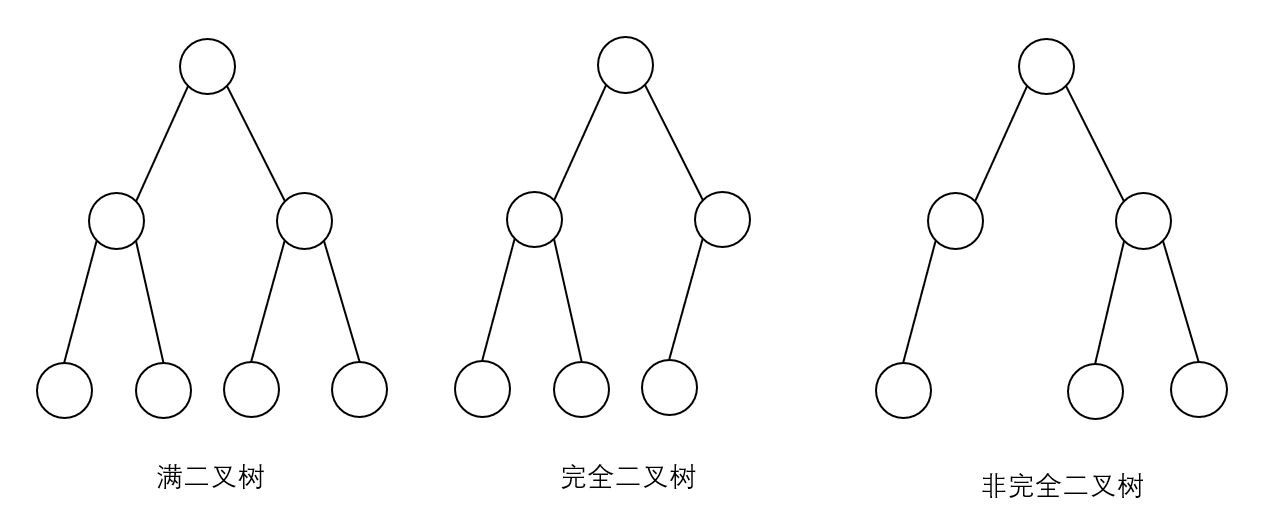
完全二叉树

在讨论堆之前，先回顾一下什么是 完全二叉树（Complete Binary Tree）。在一颗二叉树中，每一个节点都与深度为K的满二叉树中编号从 1 至 n 的节点一一对应，这样的二叉树称为完全二叉树。也就是除最底层节点外，其余层的节点都被完全填满，最底层允许不填满，但需要从左到右填充。

什么是堆（heap）

所谓堆，就是利用树的结构来维护一组数据，堆的本质就是一个完全二叉树。

如果在一颗完全二叉树中，每个节点都大于等于它的两个子节点，那么我们就说这个完全二叉树是堆有序的。一组能以堆有序的完全二叉树排序、并在数组中按层级存储的元素，我们就称为二叉堆。

二叉堆能够比初级实现更好地实现优先队列。

要点:

完全二叉树
堆有序（父节点 >= 两个子节点）
最大元素在堆顶，称为大顶堆
最小元素在堆顶，称为小顶堆

堆的性质

在一个基于完全二叉树的堆中：

如果下标从 1 开始，那么 k 的两个子节点分别为 2k 和 2k+1
如果下标从 0 开始，那么 k 的两个子节点分别为 2k+1 和 2(k+1)

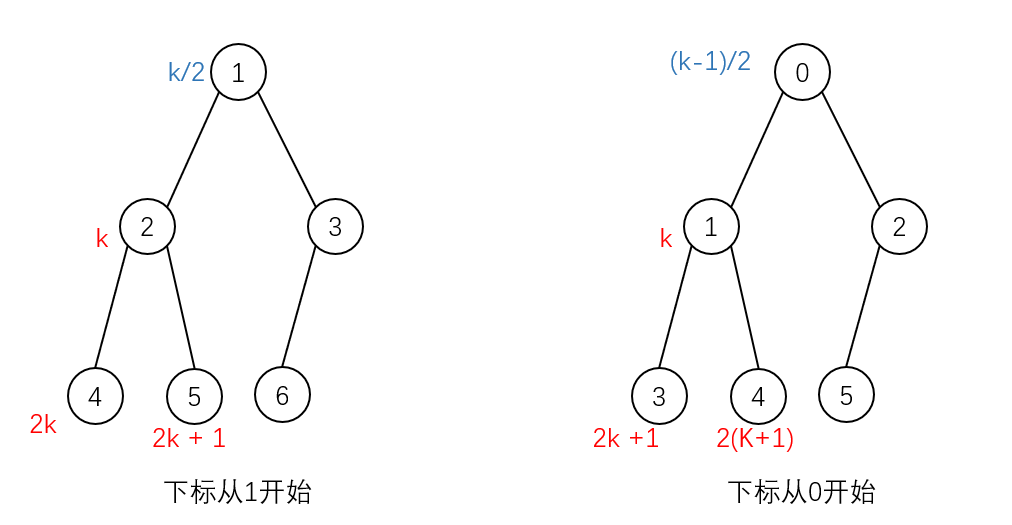
通过这个性质，我们可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。

堆的插入、删除、有序化

当你往堆中插入或删除一个元素时，怎么保证堆不会乱掉？让它继续保持有序？

插入元素：使用上浮法调整

当我们往堆中插入一个新元素时，通常插入在树的末尾（即数组末尾），然后通过跟它的父节点比较并交换的方式，一步步有序化。这种从末尾一步步往上调整的方式，称为上浮法。

小顶堆上浮法核心实现：

private void swim(int k){
    while( k>1 && less(k/2, k)){
        exch(k/2, k);
        k  = k/2;
    }
}

删除元素：使用下沉法调整

当我们从堆中删除最优先元素时，通常是删除堆顶元素，但是这样会导致整个堆乱掉。

我们可以先把堆顶元素和末尾元素（数组头和尾）先交换，然后再删除数组尾（由于已经交换，实际删除的是一开始的堆顶）。

这样一来，交换后的堆顶实际上是“违规”的顶，我们将它与其叶子节点比较，把它一步步调整下去，这种我们称为下沉法。

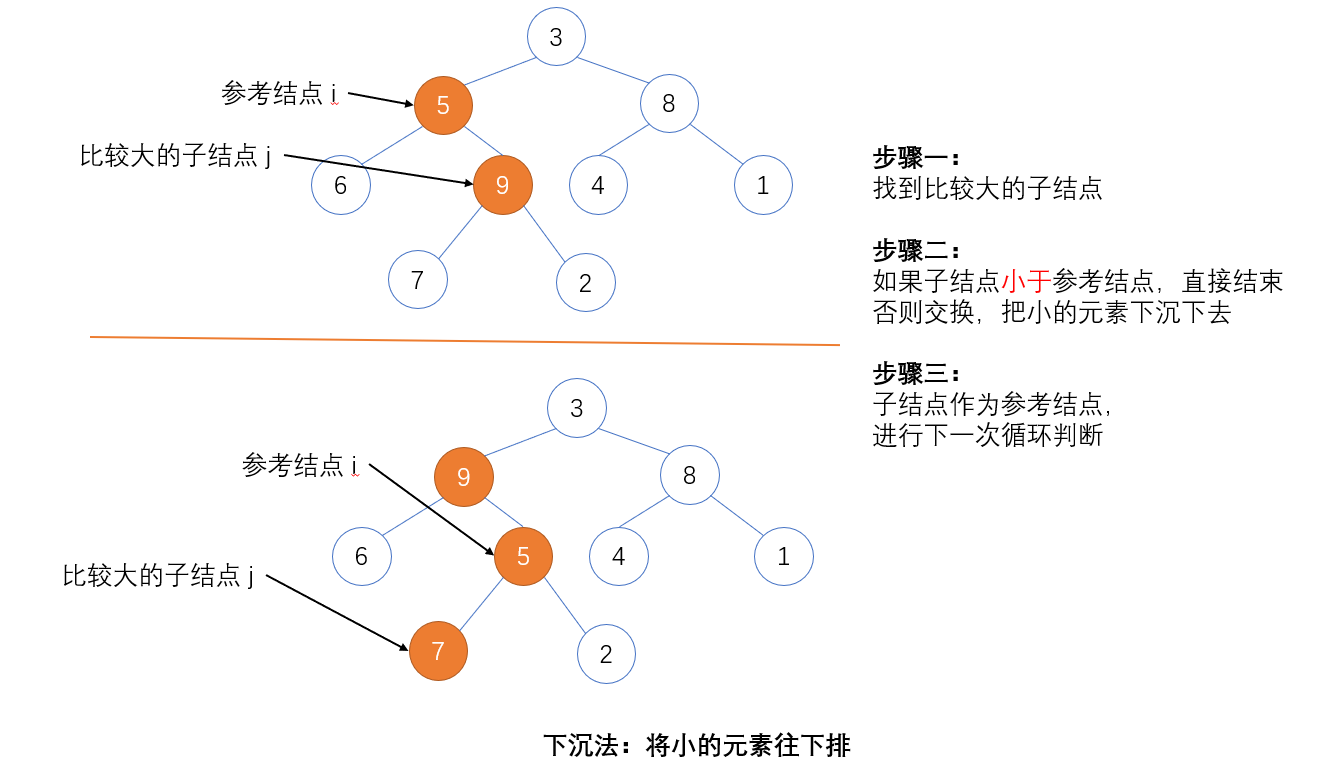
小顶堆下沉法核心实现：

private void sink(int k){

    // k 是参考节点， 2*k 是左子节点， <= N 确保子节点有元素
    while (2*k <= N){
        // j 是子节点，我们要把参考节点跟比较大的子节点做比较
        //由于不知道左子节点比较大还是右子节点比较大
        // 默认为 左子节点
        int j = 2*k;

        // 左右子节点比较，如果 左子 < 右子，j改为右子
        if ( j<N && less(j,j+1))  j++;

        // 参考节点跟比较大的子节点比较，如果子节点比较小，直接退出
        if ( !less(k,j)) break;

        // 如果子节点比较大，把比较小的参考节点沉下去
        exch(k,j);

        // 把子节点作为参考节点，继续循环
        k = j;
    }
}

基于堆的优先队列

算法 2.6

public class MapPQ<key extends Comparable<key>>{
    private key[] pq;
    private int N = 0;

    public MapPQ(int MaxN){
        pq = (key[]) new Comparable[maxN+1];
    }

    public boolean isEmpty(){
        return N == 0;
    }

    public int size(){
        return N;
    }

    public void insert(Key v){
        pq[++N] = v;
        swim(N);
    }

    public Key delMax(){
        Key max = pq[1];  //从根节点得到最大元素
        exch(1, N--);     //将其和最后一个节点交换
        pq[N+1] = null;   //防止对象游离
        sink(1);          //恢复堆有序
        return max;
    }
}

使用优先队列解决 tok-k 问题

给定一个长度为 n 的无序数组 nums ，请返回数组中最大的 k 个元素。

这个问题非常适合用优先队列解决：

先创建一个小顶堆，再将数组的前 k 个元素入堆
接下来，只要比较下一个元素和堆顶元素的大小，遇到更大的数就把堆顶换掉，直至把数组遍历完
最后，这个堆里的元素就是原数组最大的 k 个元素了。

/* 基于堆查找数组中最大的 k 个元素 */
Queue<Integer> topKHeap(int[] nums, int k) {
    Queue<Integer> heap = new PriorityQueue<Integer>();
    // 将数组的前 k 个元素入堆
    for (int i = 0; i < k; i++) {
        heap.offer(nums[i]);
    }
    // 从第 k+1 个元素开始，保持堆的长度为 k
    for (int i = k; i < nums.length; i++) {
        // 若当前元素大于堆顶元素，则将堆顶元素出堆、当前元素入堆
        if (nums[i] > heap.peek()) {
            heap.poll();
            heap.offer(nums[i]);
        }
    }
    return heap;
}

堆排序

基于优先队列的排序方法：将所有元素插入一个查找最小元素的优先队列，然后重复调用删除最小元素的操作，将他们按顺序删去。

堆排序就是一种这样的方法。分为两个阶段：

构造堆：将数组以堆的形式安排
下沉排序：按递减顺序取出所有元素，得到排序结果

算法2.7

public static void sort(Comparable[] a){
    int N = a.length;
    for (int k=N/2; k>=1 ;k-- ) sink(a, k, N);

    while(N>1){
        exch(a, 1, N--);
        sink(a, 1, N);
    }
}

优先队列不同实现的比较

实现	插入	删除	寻找最小值
无序数组	1	n	n
无序链表	1	n	n
有序数组	n	1	1
有序链表	n	1	1
二叉搜索树	logn(平均)	logn(平均)	logn(平均)
平衡二叉搜索树	logn	logn	logn
二叉堆	logn	logn	1