树和二叉树
什么是树(tree)
我们知道,链表是一种线性递归的数据结构。前一个节点指向后一个节点,线性地链接起来。树跟链表类似,只不过树的节点与节点之间,不再是单个线性地链接,而是一个节点可以指向多个其他节点。
树和链表一样,都是递归的数据结构,既然是递归的数据结构,那一棵树和其子树,其实没有本质的区别,因此很多问题都可以用递归来解决。要解决这棵树,就先解决其子树,要解决其子树,就解决子树的子树……直到没有子树了,再处理问题,然后向上返回。
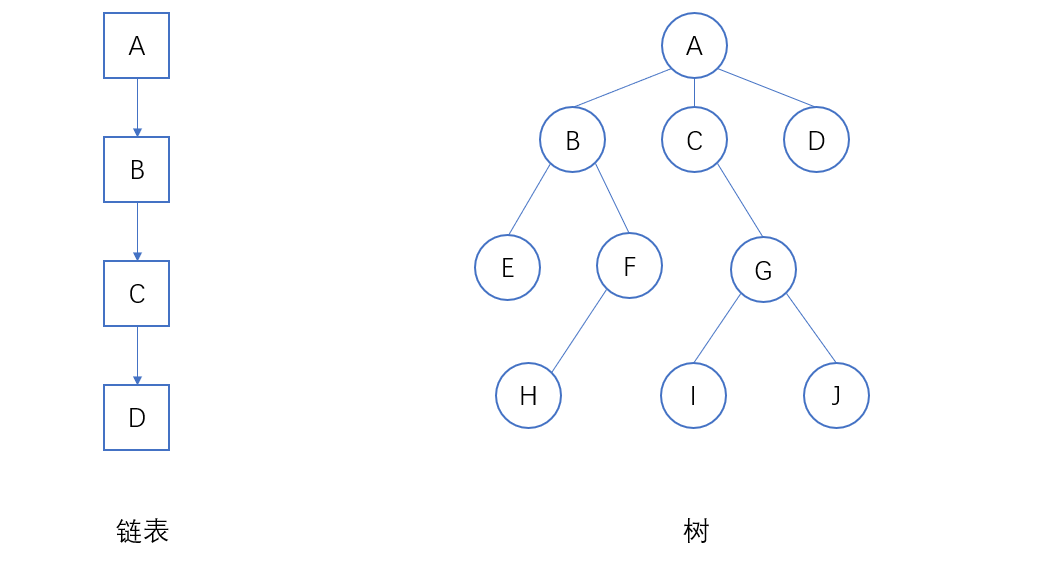
树的相关术语
- 根节点:根节点是一个没有双亲节点的节点,一棵树中最多有一个根节点
- 边:双亲节点到孩子节点的链接
- 叶子节点:没有孩子节点的节点
- 兄弟节点:拥有相同双亲节点的所有孩子节点
- 祖先节点:如果存在一条从根节点到节点q的路径,其节点p出现在这条路径上,那么就可以吧节点p叫作节点q的祖先节点,节点q也叫做p的子孙节点
- 节点的大小:节点的大小是指子孙的个数,包括其自身
- 树的层:位于相同深度的所有节点的集合叫作树的层
- 节点的深度:是指从根节点到该节点的路径长度(上图G点的深度为2,A—C—G)
- 节点的高度:节点到树中最深节点的路径长度,只含有根节点的树的高度为0。(B的高度为2,B—F—J)
二叉树(binary tree)
如果一棵树中所有的节点都只有 0,1 或者 2 个孩子节点,那么这棵树就是二叉树。
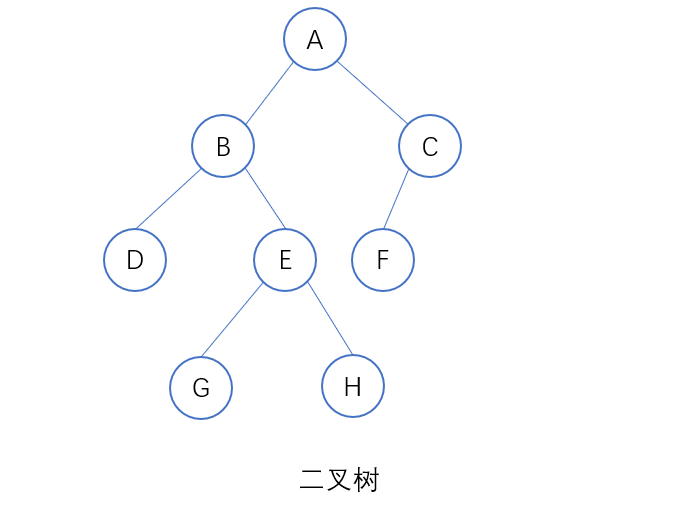
class TreeNode {
int val; // 节点值
TreeNode left; // 左子节点
TreeNode right; // 右子节点
...
}二叉树的几种形式
- 完美二叉树、满二叉树(perfect binary tree):所有层的节点都被完全填满
- 完全二叉树(complete binary tree):除最底层节点外,其余层的节点都被完全填满,最底层允许不填满,但需要从左到右填充
- 完满二叉树(full binary tree):除了叶节点之外,其余所有节点都有两个子节点
- 平衡二叉树(balanced binary tree):任意节点的左子树和右子树的高度之差的绝对值不超过 1
遍历二叉树
访问树中所有节点的过程叫作树的遍历。如果用递归的思想去进行遍历就不难理解了。
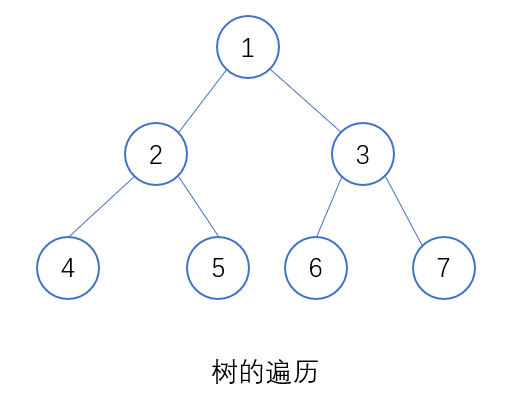
前序遍历
前序遍历的规则如下:
- 访问根节点;
- 按前序遍历方式遍历左子树;
- 按前序遍历方式遍历右子树.
上图使用前序遍历的结果为: 1 2 4 5 3 6 7
void preOrder(BinaryTreeNode root) {
if (null != root) {
System.out.println(root.getData());
preOrder(root.getLeft());
preOrder(root.getRight());
}
}中序遍历
中序遍历的规则如下:
- 按中序遍历方式遍历左子树;
- 访问根节点;
- 按中序遍历方式遍历右子树.
上图使用中序遍历的结果为:4 2 5 1 6 3 7
void inOrder(BinaryTreeNode root) {
if (null != root) {
inOrder(root.getLeft());
System.out.println(root.getData());
inOrder(root.getRight());
}
}后序遍历
后序遍历的规则如下:
- 按后序遍历方式遍历左子树;
- 按后序遍历方式遍历右子树;
- 访问根节点.
上图使用后序遍历的结果为:4 5 2 6 7 3 1
void postOrder(BinaryTreeNode root) {
if (null != root) {
postOrder(root.getLeft());
postOrder(root.getRight());
System.out.println(root.getData());
}
}二叉树的数组表示
可以用数组来表示一个二叉树。若某节点的索引为 i ,则该节点的左子节点索引为 2i + 1 ,右子节点索引为 2i + 2 ,对于树中不存在的节点,则用 null 占位。
二叉搜索树(BST)
二叉搜索树,又称二叉查找树(Binary Search Tree, BST),是一种所有左子树节点的元素小于根节点的数据,所有右子树节点的元素大于根节点数据的二叉树。
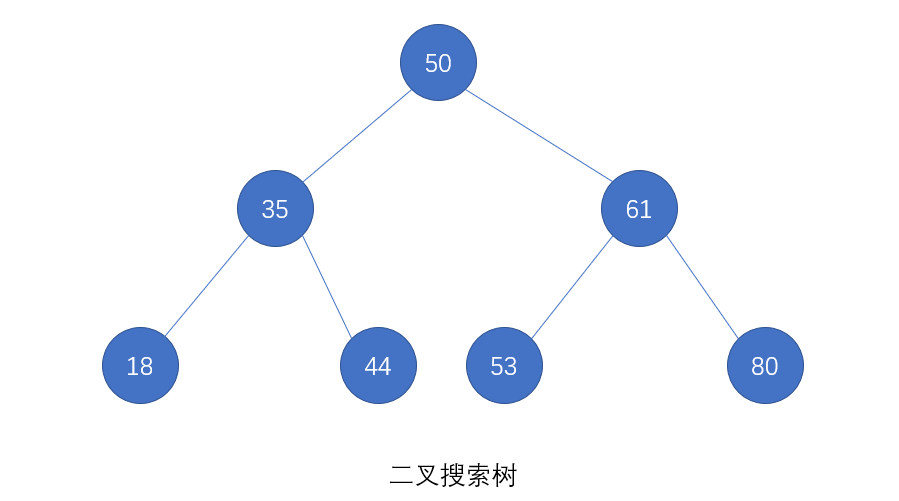
重要性质:二叉搜索树的中序遍历序列是升序的。
在 BST 中插入节点
- 插入的节点必然成为一个叶子节点
- 从根节点依次向下查找,如果要插入的节点小于当前节点,则在左子树查找,否则在右子树查找
在 BST 中删除节点
- 如果要删除的节点是叶子节点,直接找到并删除即可
- 如果要删除的节点有1个叶子节点,则把待删除节点替换为其子节点即可(需要有一个指针来记录其父节点)
- 如果要删除的节点有2个叶子节点,则把待删除节点替换为【右子树的最小节点】 或 【左子树的最大节点】(需要递归查找到最下层的叶子节点)
二叉树的应用
- 编译器中的表达式树
- 用于数据压缩算法中的赫夫曼编码树
- 支持在集合中查找、插入和删除,其平均时间复杂度为O(lognn)的二叉搜索树(BST)
- 优先队列(PQ),它支持以对数时间(最坏情况下)对集合中的最小(或最大)数据元素进行搜索和删除
参考资料:《Hello 算法》7.4 二叉搜索树
