有时候我们需要搜索信息，例如，在数组中找出某个元素，或者找出某个集中是否有某个对象。我们把寻找目标信息的过程，叫做查找。

什么是查找

顺序查找 和 二分查找 是查找的基本方法。

当我们需要高效查找时，我们可以用 符号表（或者叫字典、索引） 来表示一张抽象的表格。符号表（symbol table）是一种存储键值对的数据结构。目的是将一个键和一个值联系起来，使我们可以通过键找到值。这种数据结构包括两种操作：

1. 插入（put）：将一组新的键值对存入表中
2. 查找（get）：根据给定的键，找到相应的值

生活中不乏符号表的例子：

1. 字典：通过单词找到释义
2. 网络搜索：通过关键字找到网页
3. 账户管理：通过账号找到交易详情

在计算机科学中，有三种经典的高效符号表：

1. 二叉查找树（或者叫二叉搜索树，Binary Search Tree, BST）
2. 红黑树（基于平衡查找树, AVL）
3. 哈希表（或者叫散列表）

---

顺序查找和二分查找

顺序查找

顺序查找，简单地说，就是遍历。从顺序表中逐个与目标值进行比对，直到找到匹配元素。

public static int SequenceSearch(int[] arr, int key){

  for (int i = 0; i < arr.Length; i++){
      if (arr[i] == key){
          return i;
      }
  }
  return -1;
}

二分查找

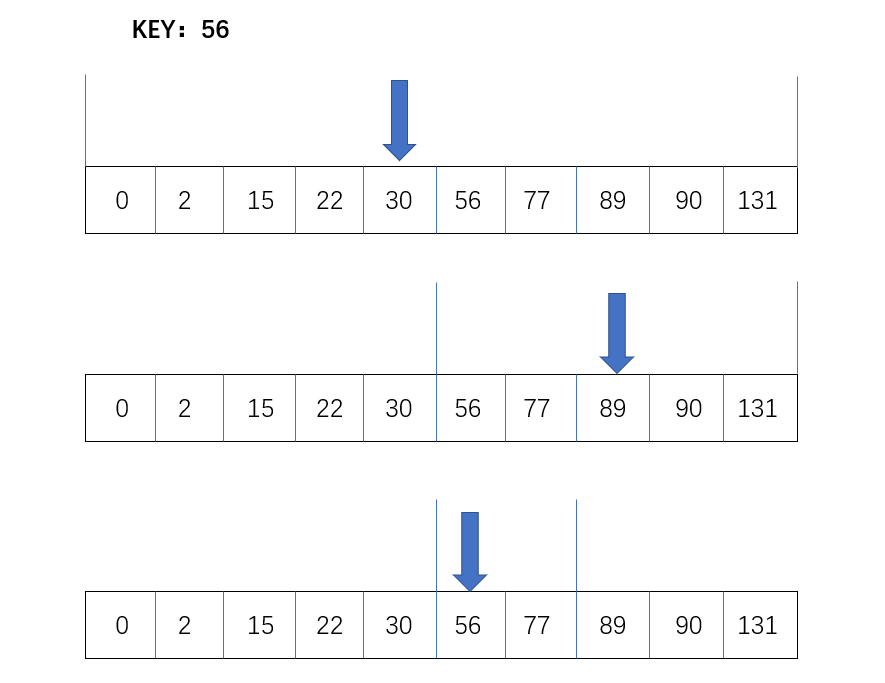
先把一个序列 从小到大排序，取中间元素与目标值进行比对，如果中间元素比目标值大，就在中间点左半边继续取中间点，否则在右半边取中间点。

import java.util.Arrays;

    public static int binarySearch(int[] arr, int target){

        int low = 0;
        int high = arr.length -1;
        int mid;

        while (low <= high){
            // 每次调整后，中间值重新计算
            mid = (low + high) / 2;

            // 如果目标值大于中间值，将 low 调整到中间+1（下一次将查找右半边）
            if (target > arr[mid]) low = mid + 1;

            // 如果目标值小于中间值，将 high 调整到中间-1（下一次将查找左半边）
            else if (target < arr[mid]) high = mid - 1;

            // 如果目标值等于中间值，返回
            else return mid;
        }

        // 没有找到，返回 -1
        return -1;
    }

    public static void main(String[] args) {
        // 前提：数组一定要是有序
        int[] testArr = {3,4,8,10,11, 66, 80, 128};

        System.out.println(Arrays.toString(testArr));

        int result = binarySearch(testArr, 128);

        if ( result == -1 ) System.out.println("没有找到目标");
        else System.out.println("在数组下标 " + result + " 处找到目标");
    }
}

---

哈希

什么是哈希（Hash）？

Hash就是把任意长度的输入通过散列算法，变换成固定长度的输出，该输出就是散列值（哈希值）。

这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来唯一地确定输入值。简单的说，哈希就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。

所有散列函数都有如下一个基本特性：根据同一散列函数计算出的散列值如果不同，那么输入值肯定也不同。但是，根据同一散列函数计算出的散列值如果相同，输入值不一定相同。

简单地说，哈希是一种把一大堆数据放到一小堆格子里的游戏。麦当劳早高峰时总喜欢在取餐处摆个架子，订单尾号为1的放在1号格子、订单尾号为2的放在2号格子......这就是一种哈希策略。可以预见，一个格子里可能存在多个订单，这就是哈希冲突。但也不用担心，我们仍可以先找到对应的架子，再根据我们的订单号“35018”拿到正确的早餐。

哈希函数

哈希函数（散列函数）就是把键转换为数组的下标的过程。对于不同数据类型的键，有不同的哈希函数方法，例如：

• 正整数：除留余数法（选择大小为素数M的数组，对于任意正整数k，计算k除以M的余数。简单地说，就是 k % M）
• 浮点数：乘以M并四舍五入得到一个 [0,M-1] 之间的索引值。（但是这样做会让高位作用大，低位作用小，解决办法是将建转换成二进制然后用除留余数法）
• 字符串：除留余数法
• 组合键：组合除留余数

当然，除了除留余数法之外，还有直接定址法、数字分析法、平方取中法等来构造哈希函数，这里不展开讲。

在 Java 中，所有数据类型都继承了一个能够返回一个 32 Bits 整数的 hashCode() 方法。每种数据类型的 hashCode() 方法和 equal()方法必须一致。也就是说，a.equal(b)返回 true，那 a.hashCode() 和 b.hashCode() 必然一致。但是反过来却不一定。

哈希表（散列表）

哈希表是算法在时间和空间上作出权衡的经典例子。

我们知道，连续的存储结构——数组，在数据的查找和修改上具有很好的优点，很方便，时间复杂度很小。但是在数据的增添和删除上则显得很麻烦，空间复杂度很大。而非连续，非顺序的存储结构——链表，恰和数组相反，数据的增添和删除容易，空间复杂度很小，查找和修改复杂，时间复杂度很大。

而哈希表，既满足了数据的查找和修改很容易，同时又不占用很多空间的特点。

使用哈希的查找算法分为两步：

1. 用哈希函数将被查找的键转化为数组的一个下标值
2. 处理碰撞冲突

为什么会碰撞冲突？因为不同的键通过哈希函数计算出来的值可能一样，比如，17%7=3，24%7=3，那对于键17和键24来说，他们的哈希结果都是3。也就是说，我们把键是17和键是24的数据都存储在了数组下标为3的地方，也就导致了碰撞冲突。

解决碰撞冲突的两种经典方法分别是：拉链法 和 线性探测法。

基于拉链法的哈希表

拉链法的处理方式是，将大小为 M 的数组中的每一个元素指向一条链表，链表中的每个节点都存储了哈希值为该元素索引的键值对。

查找分两步：

1. 根据哈希值找到链表；
2. 沿着链表顺序查找相应的键

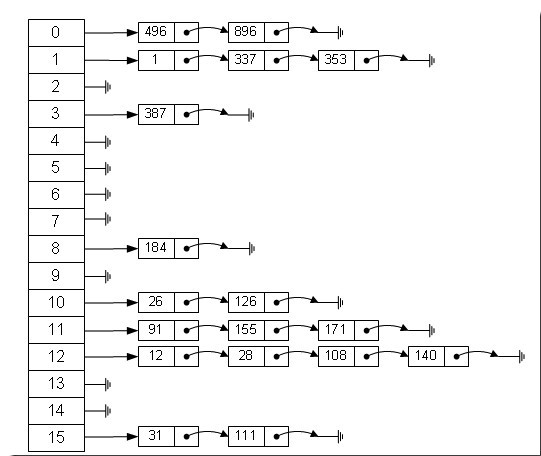
可以拿我们生活的中的字典做比喻，比如我们要查找 “哈” 这个字，我们先去目录找到“哈”在 351 页。然后我们翻开第 351 页，发现这一页还有其他的比如"蛤"、“铪”等字，我们要在这一页中找到“哈”字所在的位置。

Java 实现

public class SeparateChainingHashST<Key, Value>{
    private int N; //键值对总数
    private int M; //哈希表的大小

    // 存放链表对象的数组
    // SequentialSearchST是基于无序链表的顺序查找，实现见下面
    private SequentialSearchST<Key, Value>[] st;

    //无参构造函数
    public SeparateChainingHashST(){
        this(997); // 无参构造函数调用有参构造函数
    }

    //有参构造函数
    public SeparateChainingHashST(int M){
        //创建M条链表
        this.M = M;

        // Java不支持泛型数组，所以需要强制类型转换
        st = (SequentialSearchST<Key, Value>[]) new SequentialSearchST[M];

        for (int i=0; i<M ;i++ ) {
            st[i] = new SequentialSearchST();
        }
    }

    // 哈希函数：计算哈希值
    private int hash(Key key){
        return (key.hashCode() & 0x7ffffffff) % M;
    }

    //通过键获取值
    public Value get(Key key){
        return (Value) st[hash(key)].get(key);
    }

    //修改某个键对应的内容
    public void put(Key key, Value val){
        st[hash(key)].put(key, val);
    }

    //哈希表中所有键的集合
    public Iterable<Key> keys() {
        Queue<Key> queue = new Queue<Key>();
        for (int i = 0; i < m; i++) {
            for (Key key : st[i].keys())
                queue.enqueue(key);
        }
        return queue;
    }
}

• 基于拉链法的哈希表完整实现: SeparateChainingHashST.java

线性探测法（开放定址法）

当冲突发生时，使用某种探查(亦称探测)技术在散列表中形成一个探查(测)序列。沿此序列逐个单元地查找，直到找到给定的关键字，或者碰到一个开放的地址(即该地址单元为空)为止（若要插入，若探查到开放的地址，则可将待插入的新结点存人该地址单元）。查找时探查到开放的地址则表明表中无待查的关键字，即查找失败。

---

引申：hashcode的作用

hashCode用于返回对象的散列值，用于在散列函数中确定放置的桶的位置。

1. hashCode的存在主要是用于查找的快捷性，如Hashtable，HashMap等，hashCode是用来在散列存储结构中确定对象的存储地址的；
2. 如果两个对象相同是 equals 的，那么这两个对象的 hashCode 一定要相同；
3. 如果对象的 equals方法 被重写，那么对象的 hashCode 也尽量重写，并且产生 hashCode 使用的对象，一定要和equals方法中使用的一致，否则就会违反上面提到的第2点；
4. 两个对象的hashCode相同，并不一定表示两个对象就相同，也就是不一定适用于equals(java.lang.Object) 方法，只能够说明这两个对象在散列存储结构中，如Hashtable，他们“存放在同一个篮子里”。

---

二叉查找树（二叉搜索树，BST）

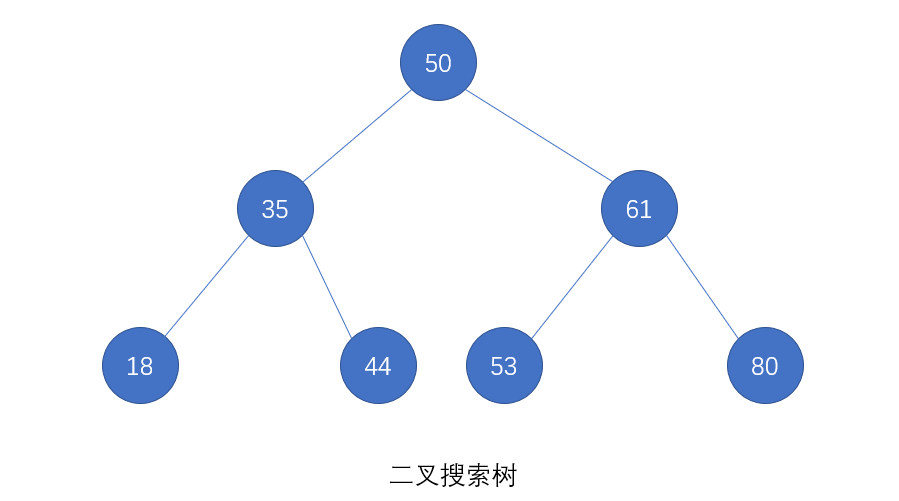
二叉搜索树，又称二叉查找树（Binary Search Tree, BST），是一种所有左子树结点的元素小于根节点的数据，所有右子树结点的元素大于根节点数据的二叉树。

注意：在 BST 中，没有键值相等的节点（no duplicate nodes）。

BST 的查找

查找方式有点类型二分查找方法，知识这里采用的树结构进行存储。首先与根结点进行判断:

1. 如果当前结点为 null，则直接返回 null
2. 如果当前结点值与查找值相同则返回当前结点
3. 如果当前结点值 < 查找值，则递归地到当前结点的 右孩子 查找
4. 如果当前结点值 > 查找值，则递归地到当前结点的 左孩子 查找

public Tree search(Tree root, int val) {

    // 1. 如果当前结点为 null，则直接返回 null
    if(root == null) {
     return null;
    }

    // 2. 如果当前结点值与查找值相同则返回当前结点
    if(root.val == val) {
     return root;
    }

    // 3. 当前结点值 < 查找值，则递归地到当前结点的 右孩子 查找
    else if (root.val > val) {
     return search(root.left, val);
    }

    // 4. 当前结点值 > 查找值，则递归地到当前结点的 左孩子 查找
     else {
     return search(root.right, val);
    }
}

---

AVL查找树

二叉树查找树在插入时没有对二叉树的深度和结构做一个调整，使得叶子结点深度不一，在查找时深度越深的结点时间复杂度越高。最坏情况下退化成为链表。

为了改进查找的时间复杂度，可以使用 平衡二叉树(AVL)，平衡二叉树使得每个结点的左结点和右结点的深度差不超过1。

平衡二叉树通过左旋和右旋，一步步调整二叉搜索树，直至平衡。

---

多路查找树(B树、B+树)

多路查找树包括 B-树 和 B+ 树。

和二叉搜索树每个结点只能存储一个元素，每个结点的孩子数不多于两个的性质不一样，多路查找树每一个结点的孩子数可以多于两个，每一个结点处都可以存储多个元素。B+树在数据库索引技术中用得较多。

B-Tree查找数据时，先在根节点二分查找，命中则直接返回数据，否则对相应区间的指针指向的节点递归进行查找。查找的时间复杂度为O(logN)。由于插入删除新的数据记录会破坏B-Tree的性质，因此在插入删除时，需要对树进行一个分裂、合并、转移等操作以保持B-Tree性质

B树 和 B+树 的区别

B树每个结点都可以存放数据，而B+树只在叶子结点存放数据。

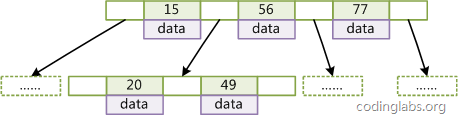
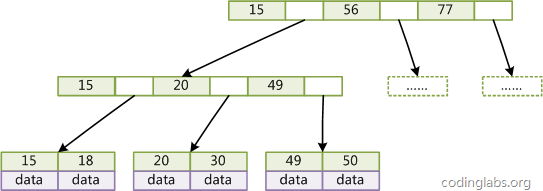
为什么B树（B+树）适合做数据库索引？

一般来说，索引本身也很大，很难将索引一次全部载入内存中，通常都是用索引文件。这样索引查找的时候也是需要I/O开销的，评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的渐进复杂度。B-Tree检索一次最多需要访问h个节点。数据库系统的设计者巧妙利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。

参考：MySQL索引背后的数据结构及算法原理

---

红黑树

红黑树是一棵二叉搜索树，它在每个结点上增加了一个存储位来表示结点的颜色，可以是RED或BLACK。通过对任一条从根到叶子的简单路径上各个结点的颜色进行约束，红黑树确保没有一条路径会比其它路径长2倍，因此是近乎平衡的。

红黑树的性质：

• 每个结点的颜色只能是红色或黑色的。
• 根结点是黑色的。
• 每个叶子结点（NIL）是黑色的。
• 如果一个结点是红色的，那么它的两个子结点都是黑色的。
• 对每个结点，从该结点到其所有后代叶子简单的简单路径上，均包含相同数目的黑色结点。